1989. Максимальное паросочетание

Граф G = (V, E) называется двудольным, если множество его вершин V можно разбить на два подмножества A и B так, что любое ребро из E соединяет вершину из A с вершиной из B.

Паросочетанием P называется любое подмножество E, такое что никакие два ребра из этого множетва не имеют общих вершин.

Максимальное паросочетание – это паросочетание, содержащее максимальное количество рёбер.

Найдите максимальное паросочетание в заданном двудольном графе.

Вход. В первой строке заданы три числа n, m и k (1 ≤ n, m ≤ 100, 1 ≤ k ≤ 10000), где n – число вершин в множестве A, m – число вершин в множестве B, а k – количество рёбер в графе. Каждая из следующих k строк содержит по два числа u_i и v_i, обозначающих, что вершина u_i из множества A соединена с вершиной v_i из множества B. Вершины во множествах A и B нумеруются независимо, начиная с единицы. Все входные числа целые.

Выход. В первой строке выведите количество l рёбер в максимальном паросочетании. Далее выведите l строк, каждая из которых содержит два числа: a и b, где a – вершина из множества A, а b – соответствующая ей вершина из множества B в паросочетании. Взятые рёбра должны образовывать максимальное паросочетание.

Пример входа	Пример выхода
2 3 4 1 1 1 2 2 2 2 3	2 1 1 2 3

РЕШЕНИЕ

максимальное паросочетание

Анализ алгоритма

Классическая задача о максимальном паросочетании, которую можно либо свести к потокам на графе, либо решить при помощи алгоритма дополняющего пути.

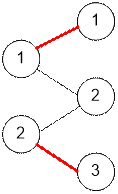
Пример

Входной граф и максимальное паросочетание имеет вид:

Реализация алгоритма

Рассмотрим алгоритм дополняющего пути без оптимизации. Граф храним в списке смежности g. Для отмечания в поиске в глубину пройденных вершин используем массив used. Для хранения текущего паросочетания используем массив mt.

#define MAX 110

vector<vector<int> > g;

vector<int> used, mt;

Функция dfs ищет дополняющий путь из вершины v поиском в глубину и возвращает 1, если такой путь будет найден. В случае нахождения увеличивающей цепи производится чередование паросочетания вдоль нее.

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int to : g[v])

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

return 1;

}

return 0;

}

Функция AugmentingPath находит максимальное паросочетание.

void AugmentingPath(void)

{

Изначально текущее паросочетание пусто.

mt.assign (m + 1, -1);

Запускаем поиск дополняющего пути из каждой вершины левой доли. Предварительно обнуляем массив посещенных вершин used.

for (int i = 1; i <= n; i++)

{

used.assign(n + 1, 0);

dfs(i);

}

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d",&n,&m,&k);

g.resize(n + 1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

Запускаем алгоритм поиска максимального паросочетания.

AugmentingPath();

Размер максимального паросочетания вычисляем в переменной flow.

flow = 0;

for (i = 1; i <= m; i++)

if (mt[i] != -1) flow++;

Выводим величину максимального паросочетания.

printf("%d\n",flow);

Выводим само максимальное паросочетание.

for (i = 1; i <= m; i++)

if (mt[i] != -1) printf("%d %d\n",mt[i],i);

Реализация с оптимизацией

#include <cstdio>

#include <vector>

#include <algorithm>

using namespace std;

vector<vector<int> > g;

vector<int> used, mt, par;

int i, j, ptr;

int n, m, k, a, b, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = to;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign (m+1, -1);

par.assign (n+1, -1);

for (run = 1; run; )

{

run = 0; used.assign(n+1, 0);

for (i = 1; i <= n; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

scanf("%d %d %d",&n,&m,&k);

g.resize(n+1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

AugmentingPath();

for (flow = 0, i = 1; i <= m; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

for (i = 1; i <= m; i++)

if (mt[i] != -1) printf("%d %d\n",mt[i],i);

return 0;

}